ECFD workshop, 6th edition, 2022

Description

ECFD6 workshop logo.

• Event from 23th of January to 3rd of February 2023
• Location: Hôtel Club de la Plage, Merville-Franceville, near Caen (14)
• Two types of sessions:
  • common technical presentations: roadmaps, specific points
  • mini-workshops. Potential workshops are listed below
• Free of charge
• More than 60 participants from academics, HPC center/experts and industry.

• Objectives
  • Bring together experts in high-performance computing, applied mathematics and multi-physics CFDs
  • Identify the technological barriers of exaflopic CFD via numerical experiments
  • Identify industrial needs and challenges in high-performance computing
  • Propose action plans to add to the development roadmaps of the CFD codes

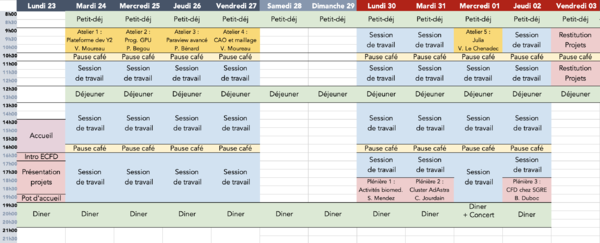
Agenda

Thematics / Mini-workshops

These mini-workshops may change and cover more or less topics. This page will be adapted according to your feedback.

Projects

Numerics - S. Mendez, IMAG & M. Bernard, LEGI

• Sub-project 1: Multi-level domain decomposition method (DDM) for coupled systems of differential-algebraic equations (A. Quirós Rodrígues, V. Le Chenadec)

The numerical approximation of multi-physics problems gives rise to complex linear systems, the solution of which leverages preconditioning techniques such as multi-grid or domain decomposition methods. This project aimed at coupling two Julia packages that being actively developed: a two-dimensional Navier-Stokes solver for free-surface and two-phase flows (Flower.jl) on the other, and a Domain Decomposition package for Cartesian grids (DDM.jl). The decomposed matrix-vector product was optimised to reduce the overhead associated with halo exchanges. The implementation of a deflated Conjugate Gradient as well as one- and two-level Additive Schwartz Method were also completed and shown to significant reduce the number of iterations for inverting monolithic systems (i.e. without resorting to operator splitting), shown to be independent of the number of subdomains for constant property flows. Future work will focus on a further optimisation of the implementation for vectorisation and multi-threading, and extension of the deflation to generalised coarse spaces to support highly discontinuous transport properties (GenEO).

• Sub-project 2: Ghost fluid method (GFM) for Electrodeformation (A. Spadotto , S. Mendez)

According to the Leaky Dielectric Model, red blood cells (RBCs) are subject to a force which is proportional to the jump of Maxwell tensor. This latter is a quantity scaling as the square of the electric field, which under the quasi-static hypothesis is defined as the gradient of the electrostatic potential. To work out the potential, an elliptic interface problem must be solved, taking into account the presence of the RBC membrane. The aim of the project was implementing the Ghost Fluid Method (GFM) to face the interface problem. Good results were obtained on unstructured meshes. Secondly, a gradient calculation was performed applying the Green-Gauss scheme, modified in the style of GFM. Future work will focus on interpolation of the gradient field onto the membrane to get an estimation of the effort. Possibly, high-order schemes for the gradient calculation will be explored. In a second time, the effort calculation will be merged into an Immersed Boundary solver for the RBC dynamics.

• Sub-project 3: Optimization of the high order framework (HOF) for Navier-Stokes incompressible (M. Bernard, P. Bégou, G. Lartigue, G. Balarac)

Over the past years, a framework has been developed to improve the spatial accuracy of numerical schemes on distorted meshes. However, even if the solution is more precise, the computational cost of the overall resolution of Navier-Stokes equations is large. As a consequence, HOF becomes profitable only on thin meshes thanks to a better spatial convergence order. The code has been analized with different analysis tools (MAQAO, Gprof, Scalasca). The main time consuming routines have been identified and improved. Moreover, some algorithms have been refactors such that the resolution of Navier-Stokes equations has been speed-up by a factor 2.5.

• Sub-project 4: Force coupling method (FCM) for particulate flows (C. Raveleau, S. Mendez)

• Sub-project 5: Breaking limitations of the linearized implicit time advancement (T. Berthelon, G. Lartigue, G. Balarac)

• Sub-project 6: Development of a traction open boundary condition (TOBC) in Yales2 (J.B. Lagaert, Guillaume Balarac)

• Sub-project 7: Development of new spatial differential operators in Yales2 (M. Bernard, G. Lartigue)

It exists different philosophies for computing differential operators on distorted meshes. In a HPC context, the 2 main approaches are the Green-Gauss operators and the Least-Squares operators. During ECFD#6, 2 new types of "non-compact" Hessian operators have been implemented by computing successively the gradient operator, eather with Green-Gauss gradient, or with Least-Squares gradient. Those operators lead to good convergence order, even on distorted mehes. However, their application on low-resolution signals lead to large error magnitude due to their extended stencil.\\ Another pair of gradient \& hessian Least-Squares operators have been implemented, leading to 2nd and 1st order accuracy for the gradient and hessian respectively. Those operators have very interesting characteristics as their stencil is restricted to the direct neighbors only and their computational cost remains low.

• Sub-project 8: DOROTHY optimization (M. Roperch, H. Mulakaloori, G. Pinon, P. Bénard)

• Sub-project 9: Anamika, a tool to improve programming productivity (K. Mohana Muraly, G. Staffelbach)

Turbulence - P. Benard, CORIA & G. Balarac, LEGI

• Sub-project 1: Explore hybrid RANS/LES strategies (T. Berthelon, G. Balarac)

For complex industrial applications, LES can still lead to a too long restitution time. In other hand, statistical approaches can lead too a lack of accuracy. In this project, the potentiality of hybrid approaches combining both have been explored. Conventional hybrid RANS/LES approaches consider a unique solution field, with an unique transport equation and a clusre terme modeled using RANS or LES models depending of the regions. The main idea is to evaluate a strategy based on a separation between mean fields and fluctuations with distinct coupled transport equations. First elements of validation using YALES2 code are shown that it was possible to correct the prediction of a RANS models, by performing LES of the fluctuations. Next steps should be to consider disctinct meshes, or even computational domains for RANS and LES with this strategy.

• Sub-project 2: Flow Instabilities over Rotating curved Surfaces (S. Sawaf, M. Shadloo, A. Hadjadj, S. Moreau, S. Poncet)

For evaluating the effect of the clearance between the blade tip and the casing of axial ducted fans on noise emissions, LES offers excellent tool to capture the consitricted flow around the blade tip especially for small clearances where RANS fails because of unsteady flow conditions. LES simulation of the aerodynamics is the first step toward extracting accoustics data that helps to improve the design of axial ducted fans so they comply with the noise emission regulations in admistrative buildings. noise emmisions are estimated using analytical aeroacoustic models informed by data that are extracted from the LES simulations.

• Sub-project 3: Automatic statistical convergence metric (C. Papagiannis, G. Balarac, O. Le Maitre, P. Congedo)

Statistics accumulation can be an important part of the restitution time in unsteady simulations (DNS/LES). In this project, the goal was to estimate uncertainties on the "finite time statistics". For time correlated data, it can be shown that the variance of the mean estimator (i.e. the fluctuation of the estimation of the mean) is dependent of the correlation time. Modeling this correlation time based on the integral time scale of the turbulence appears as a first way to define a practical metric to evaluate the statistic convergence on-fly during simulations. Next step should be to explore procedures to accelerate the statistics accumulation step.

• Sub-project 4: Wall law for Immersed Boundaries & Rough surfaces (M. Cailler, A. Cuffaro, P. Benez, S. Meynet)

Conservative Lagrangian Immersed Boundaries (CLIB) are now a useful way to take into account complex geometries in YALES2. During the workshop, a brand-new data-structure for modular and generic immersed-body has been developed. This data-structure paves the way for various new capabilities for IB methods: penalization mask shape optimization for improved velocity imposition, better control of near wall discretization based on a reliable evaluation of wall units, wall-modeling, etc... For this purpose the periodic hill test case has been considered. Simulations of this configuration has been performed by using body-fitted meshes, and CLIB for both smooth and rough surfaces. This will allow to assess the accuracy of the IB methods, and will constitute a database for IB models improvement, and the development of wall-modeling strategies.

• Sub-project 8: Atmospheric flow (U. Vigny, L. Voivenel, P. Benard, S. Zeoli)

Atmospheric flow such as Atmospheric Boundary Layer (ABL) and thermal stratification have an impact on wind turbines aerodynamic and wakes. Mostly at a wind farm scale, the change of wind turbine wake size and recovery can modify the global power production. During the workshop, the Coriolis force implementation has been validated through neutral case (where no thermal stratification i.e. no temperature gradient). It also allowed to validate the pressure forcing term, needed to drive the flow in a periodic box. YALES2 results showed a good agreement with other numerical and experimental results. Afterwards, the stable case (i.e. temperature gradient downwards) has been studied. A surface temperature as boundary condition has been developed. Yet, results are not as expected and further investigation is needed.

Two Phase Flow - C. Merlin, Ariane Group & M. Cailler, Safran Tech

• Sub-project 1: Convergent computation of interface curvature (G. Ghigliotti, M. Benard, G. Balarac, J. Carmona, R. Mercier, G. Lartigue)

Though Level-set distance evaluation through GPMM (Janodet et al., 2022) converges at order 2, the interface curvature convergence is as best 0 using the non-compact Goldman formulation. Following progresses obtained during ECFD5, a strategy based on parabolic fit of the interface has been explored during the workshhop. This method aims at fitting a parabola through least squares using the interface markers stored in the interface vicinity. First the method was applied on a 2-D perfectly spherical droplet with exact projection of the marker on the circle. This results in a first order convergent curvature. Without projection of the markers, the fiting strategy allows a slight decrease of the error but no improve on the curvature convergence order in comparison with the standard non-compact formulation. As a persective, these results will be validated on dynamic and 3-D cases (MMG3D meshes). Also, the sensitivity on the number of markers and their redundancy will be investigated.